Game trees

It turns out I was wrong - the algorithm is not just trying to minimize the number of colors, but more specifically it must minimize the unique voxel+bond combinations.

Last week, my labmate Eric Shen showed me how the origami was actually made. He showed me the pre-made vials which they ordered the origami in, and I helped to pipette certain bond colors onto the DNA octahedra wireframe solution. It felt oddly anticlimactic - to see that the actual physical reality of my hundreds of hours of work and toil - this problem which I had conceptualized as one with gigantic colored balls with sticks - to see that it really all came from this clear, water-like solution that we stick into an orb like machine vaguely reminiscent of a centrifuge from my high school chemistry classroom, or the swimsuit drying machine at my hometown swimming pool.

A centrifuge

The swimsuit drying machine

But - I had written the code to minimize the number of colors, without care to the proper orientation (+/-) of the colors within the lattice design.

Which is to say, the final result needs to be changed somehow.

The Problem

Here is again a 2D version of the problem.

Recall back to the previous post if you want a refresher on what exactly the problem is which the algorithm is trying to solve.

Input: Sub-optimal origami

Currently, the algorithm outputs a solution with the optimal number of colors, but a sub-optimal number of unique origami.

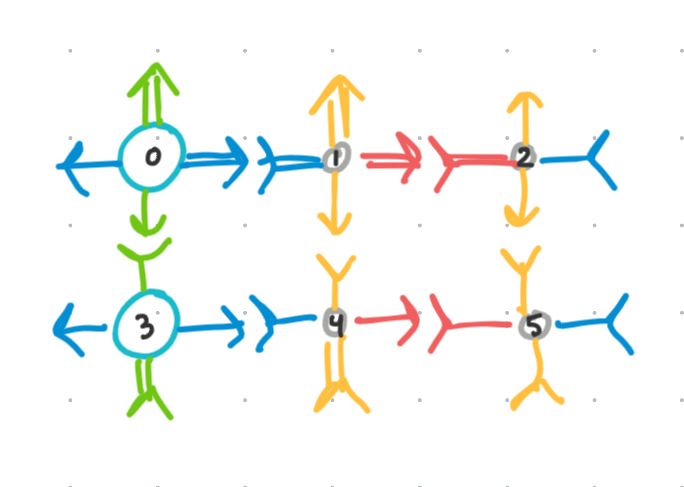
However, while this is a minimal number of colors, we still have 6 distinct unique origami (voxel+bond) combinations. All the colors are in the correct locations, but…

Goal:

By flipping the complementarity of voxel 2, we get a coloring which produces only 4 unique origami.

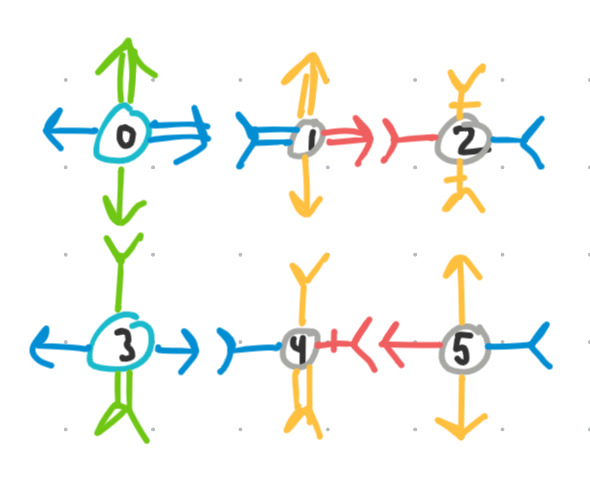
This distinction matters because it is the entire origami unit itself which moves around in the machine and attaches to other origami, not just the bonds. So in the above case, if voxel 5 were to accidentally bind on top of voxel 1, we would encounter a possible binding error where now another copy of voxel 3 cannot bind on top of voxel 0 without breaking the complementarity rule at the +/-x vertices.

If we assume that all interactions between bonds with valid opposing complementary colors are equally likely to occur, then we want to design it in such a way which minimizes the space of possible unfavorable interactions in the first place.

“Post-processsing”: Game tree optimization

Seeing that the variable space was not that large to begin with, I wondered - could we approach it like a combinatoric problem?

If we assume that all the colors are in the correct locations, then it seems like it would be a simple matter of guessing and checking different complementarities within each color until we get a minimum unique set of origami?

There is the constraint that since there cannot be palindromic sequences, and since flipping the complementarity of one bond affects its partner as well, these two binding rules combined make it so that changing just one bond can lead to a cascade of changes within the lattice.

• For instance, if we flip the +X blue bond for voxel 3, then not only does it affect the -X blue for voxel 4, but it also forces the -X bond on voxel 3 to also flip to avoid the palindromic binding.

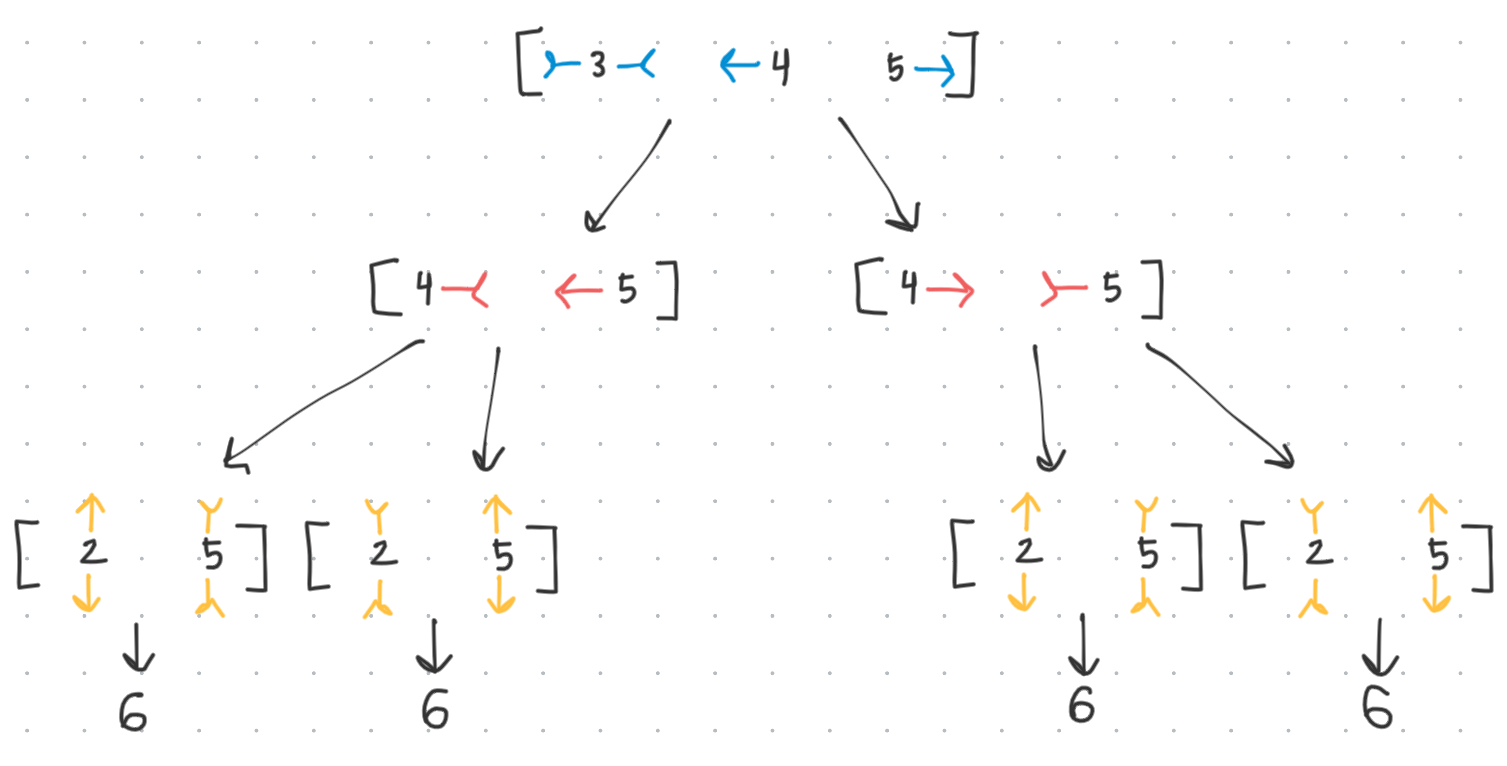
Hence, I defined a “comp_config” in my code, which represents a particular possible configuration of complementarities for a given color. If we apply the full color set of comp_configs onto the lattice we can recreate the lattice. The goal is to create a swappable set where we can easily choose comp_config 1 or 2 and have it only affect the complementarity of the colors within itself.

With these comp_configs, we can simply build out a tree of all possibilities of what complementarity the bond colors could be in, and evaluate at the bottom of each branch the number of unique origami that such a configuration would create.

A-side:

B-side:

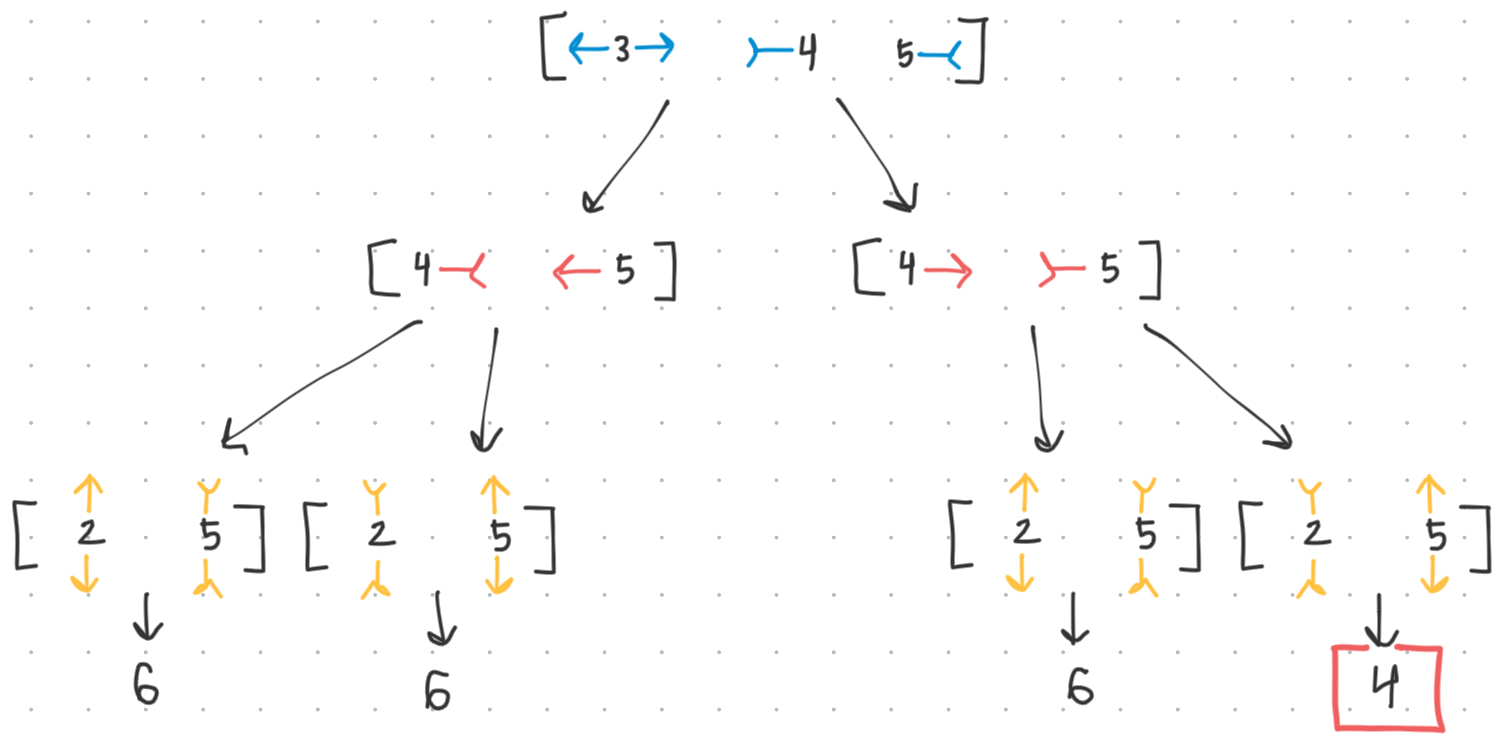
The idea of a game tree is something that I had learned in AI last semester - it feels surreal to get to implement one myself. I’ll update on the results of it soon.