Balls and sets: Topological logic gates

In my Modern Analysis class, we went over a significant amount of basic topology. I was confused at first, but I found it ultimately gave us a toolkit of concepts with which we could rigorously prove things about continuity, differentiation, and integration.

In this post I hope to go over the basic terminology and concepts we learned.

The ball

A basic building block of topology is the ball $B_r(x)$. It has a radius $r$ and is centered around some $x$ value.

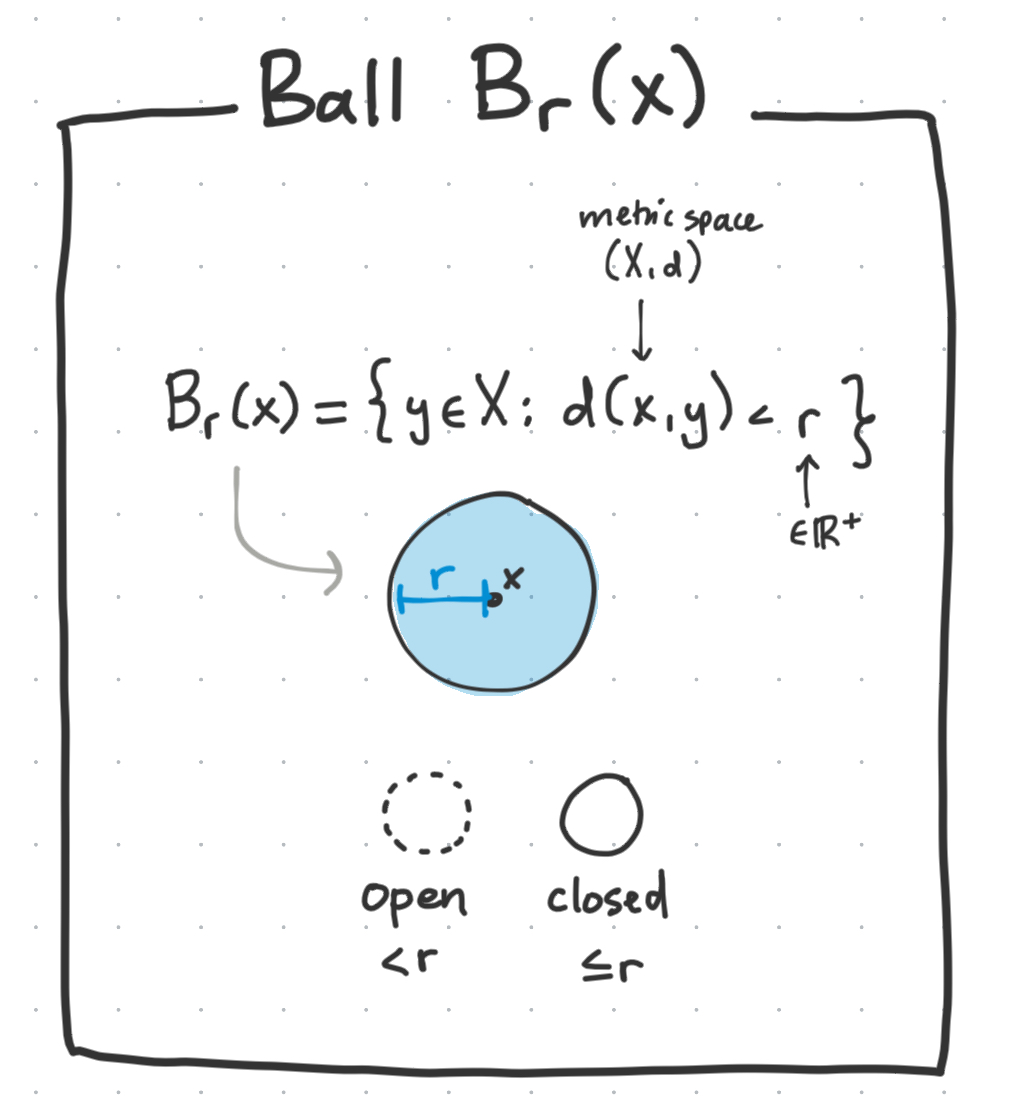
We can have open and closed variants, which we will discuss the meaning of in more detail later but for now can intuit as being:

• open: $<r$
• closed: $\leq r$

Some specific types of balls:

• The 1D ball is an interval
• The 2D ball is a circle
• The 3D ball is a sphere
• The 4D ball is a hypersphere
• Etc…. we can form any arbitrary N-dimensional ball

Open and closed sets

Open sets

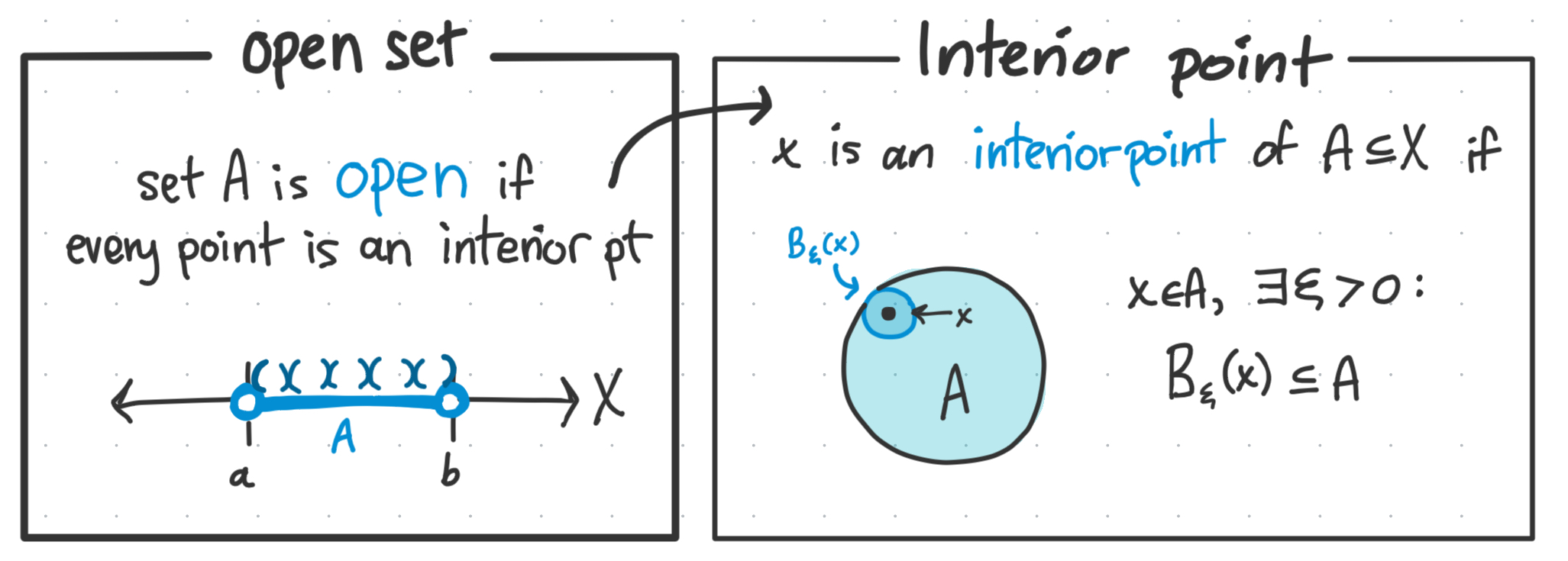
A set $A$ is open if every point $x \in A$ is an interior point.

What is an interior point?

Basically, $x$ is an interior point of $A$ if you can construct some $\varepsilon$ ball around $x$ such that it the entire ball is contained in $A$.

Closed sets

A set $A$ is closed if every limit point of $A$ is contained $\in A$.

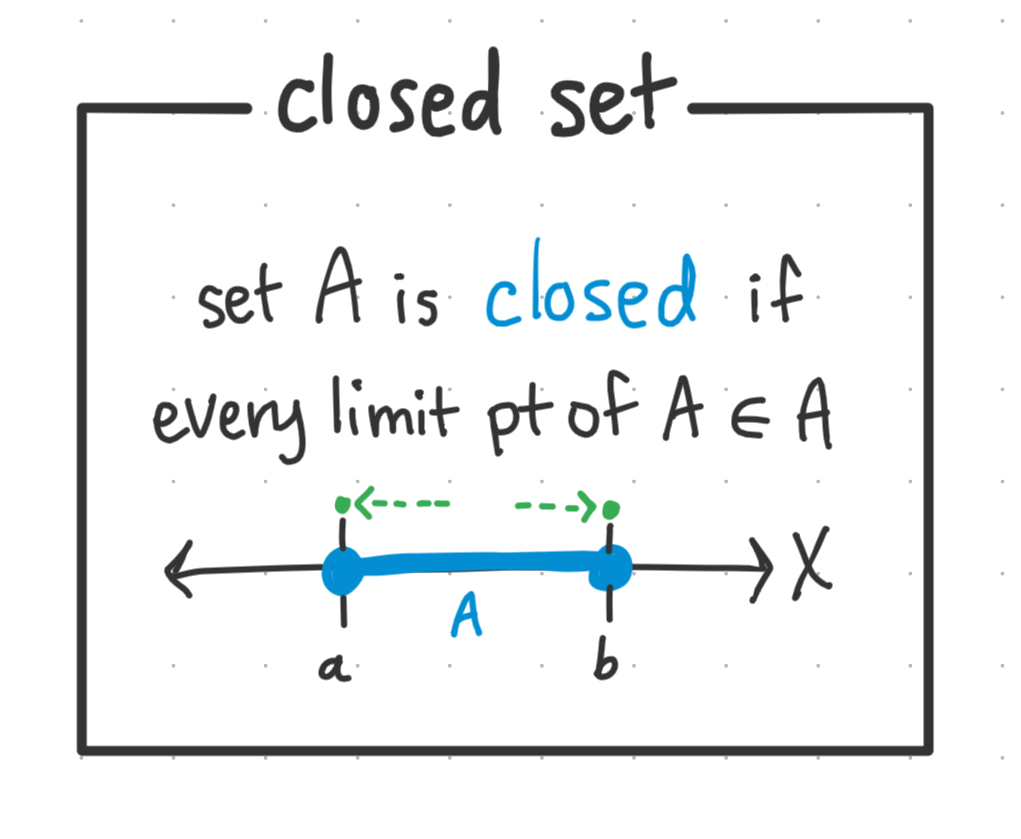
What is a limit point?

There are two definitions - I learned the topological definition first but honestly it makes way more sense with sequences - I’ll explain both.

1. $x$ is a limit point of $A$ if for all $\varepsilon$ balls around $x$, you can always find some point $y \in B_\varepsilon(x)$ such that $y \in A$.

Which okay, it’s trying to say that if you can find some point that A approaches with super close epsilon distance, and that point is not contained in A, then the set is not closed.

• Ex: So the open interval $A=(0, 1) \in \mathbb{R}$ is not closed because $0$ and $1$ are both limit points of $(0,1)$ which are not contained in $A$. Since, at the boundaries you can always find some epsilon ball super close to $0$ or $1$ that contains a point in $A$ but $0$ and $1$ are not contained within $A$ itself.

However, for me this definition only started making sense once I learned this alternate definition using sequences.

1. $x$ is a limit point of $A$ if there exists some sequence fully contained within $A$ that converges to $x$.

Eg, $x$ is the ‘limit’ of some sequence in $A$. This is so much more intuitive in my opinion and is closer to why they chose the name “limit point” in the first place. Yet I didn’t learn this definition until halfway through the semester.

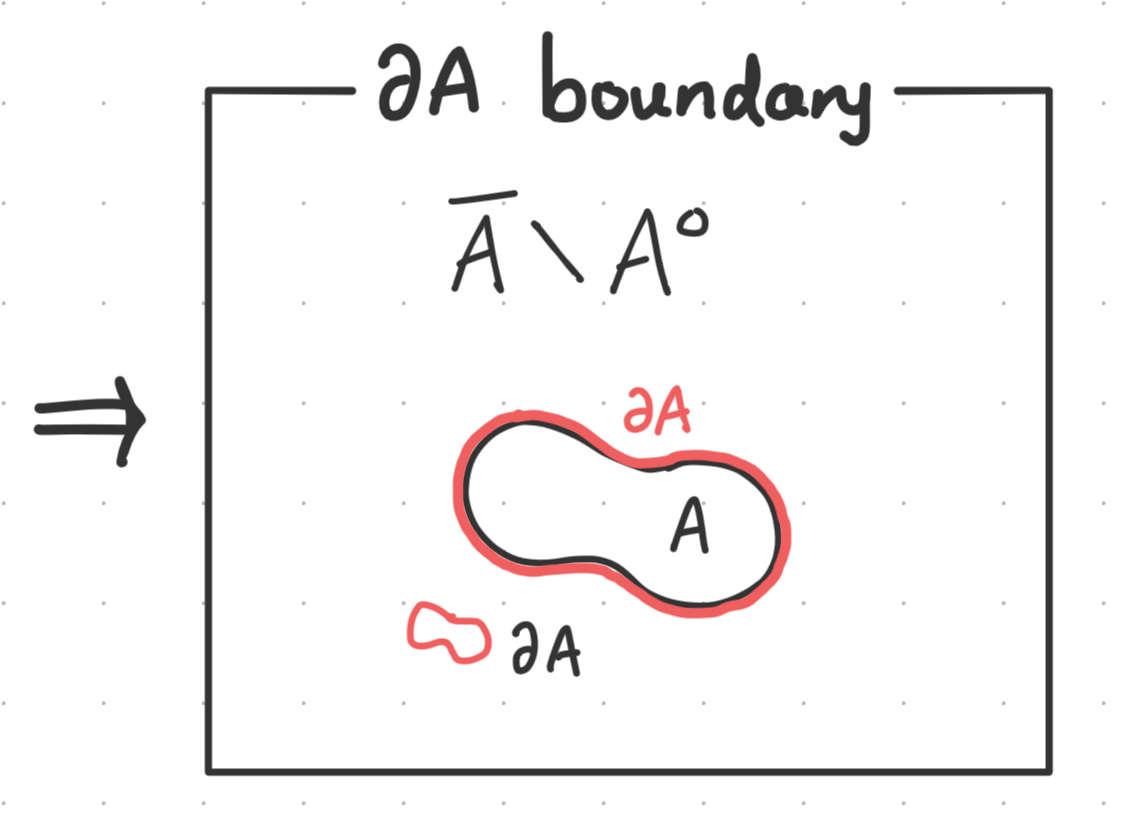
Interior, closure, boundary

The interior of A is, aptly named, for being the set of all interior points of A. We denote it as $A^o$ which we can remember since interior points are defined with the balls being inside A.

The closure of A is defined as the union of A and the set of its limit points. Which is to say, that it’s A + everything within some epsilon boundary of A. We denote it as $\bar A$ which looks symbolically fitting as A plus the little boundary hat around A.

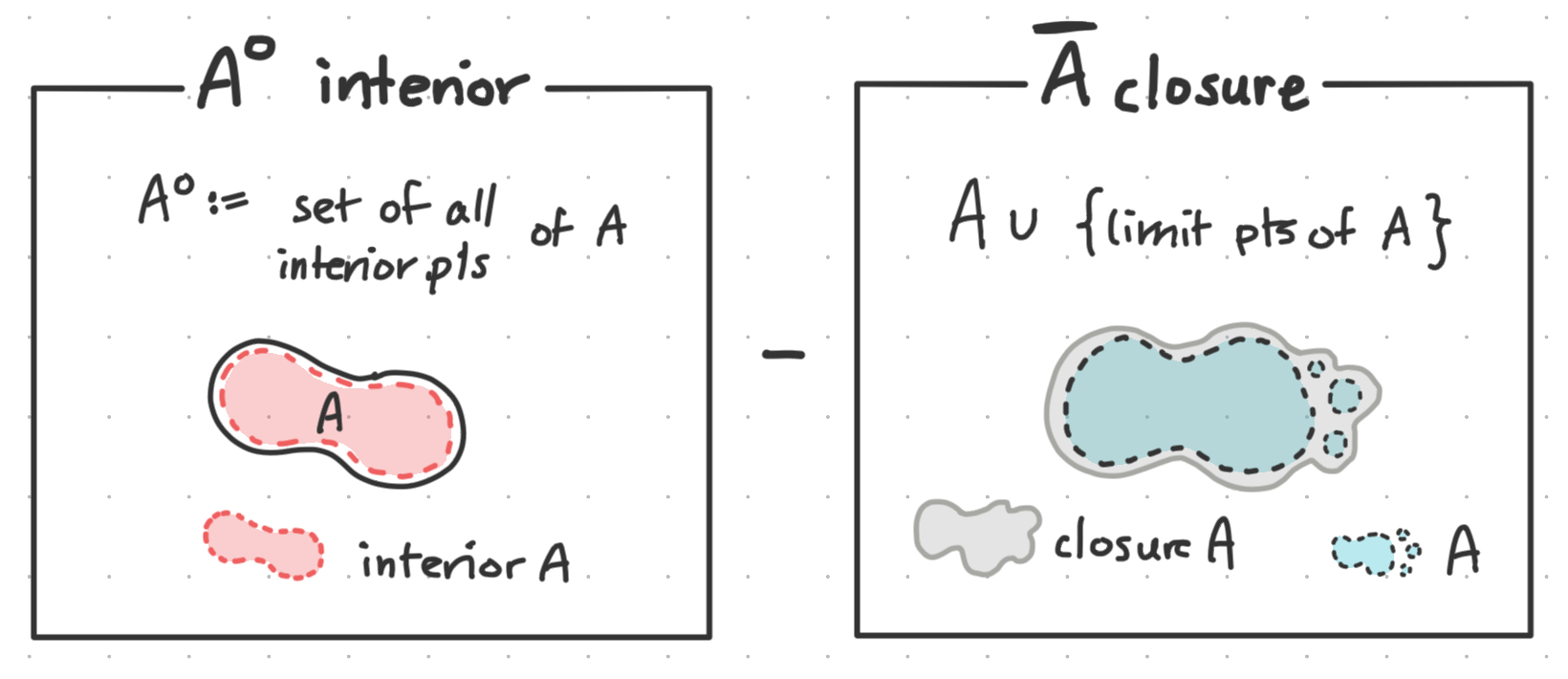
And finally, the boundary of A is the closure of A without the interior points of A. It looks kind of like drawing an actual ‘boundary’ outside of the set, such that the points here are only somewhat close to A but not surrounded by A.