Compactness

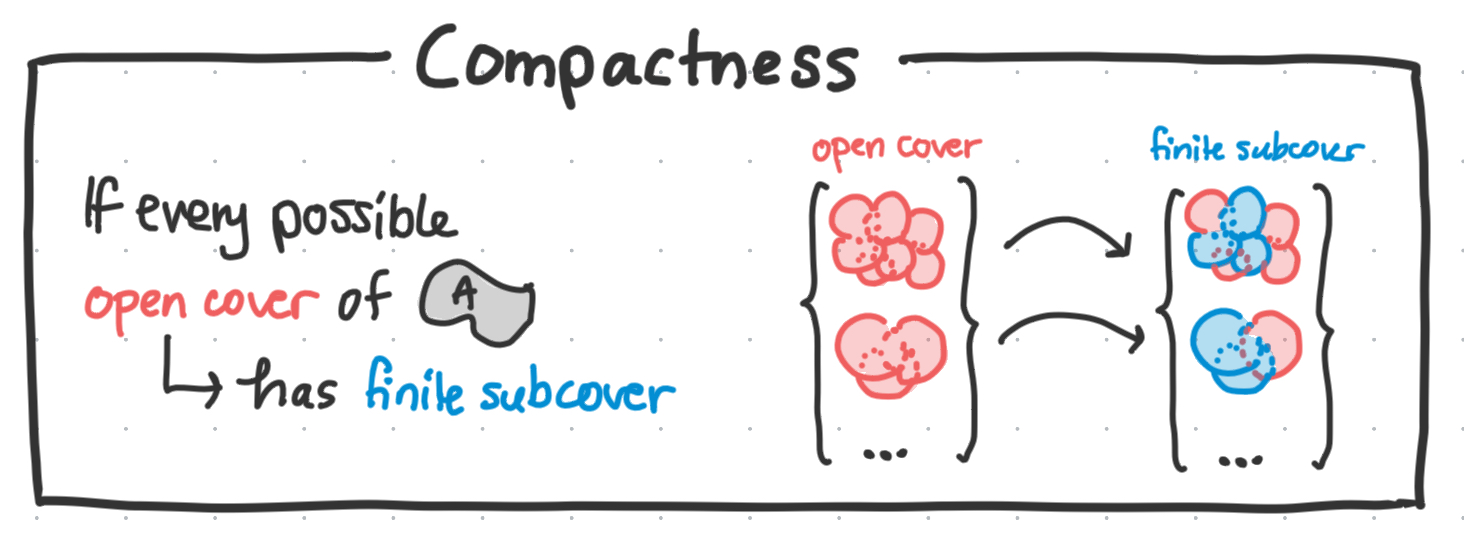
A compact set is one where every open cover has a finite subcover. WTF?

In my analysis course, our professor would always joke about compactness being our “favorite subject”. It’s a topic which is not very intuitive but so ubiquitous and useful that you start to bash your head against the wall if you don’t understand it.

I think I finally get it, but it took a lot of drawings and a lot more staring at pictures of balls before it clicked.

So, let’s step back and define it.

Compactness: The setup

The set, in the space

Take a set $A$ in the metric space $(X, d)$, such that $A \subseteq X$.

“Every open cover has a finite subcover.”

So what is an open cover?

Open covers

An open cover is any family of sets ${ G_\alpha }$ such that all sets $G_\alpha$ in the family are open, and the union of all the sets ‘covers’ $A$ completely, eg, \(A \subseteq \bigcup_{\alpha} G_\alpha\)

Subcovers

A subcover is any ‘sub’set of a cover that still covers $A$. So the subcover of an open cover is some subset of open covers which still covers A.

A finite subcover is a subcover that has finite cardinality, eg it is made up of a finite number of open covers.

So what does this mean for compactness? What does it mean that every open cover has a finite subcover?

Another way of putting this, is that you cannot construct some infinite family of sets which uniquely covers $A$, such that taking away any number of open sets to make the open cover finite would make it no longer fully cover $A$.

Putting it together

Putting it all together, we can construct a quasi-visual intuition for the notion of compactness which explains the open cover / finite subcover business.

Ex: The open ball is not compact

For example, take $A$ as the open unit ball $B_1(x)$ in $\mathbb{R}^2$. We can construct the following open cover of $A$: \(\bigcup^\infty_{n=2}B_{1-\frac{1}{n}}(x)\) which fully covers $A$ but we can’t take away any finite subfamily of covers within the open cover (eg, there exists no finite subcover) such that $A$ is still totally covered.

Why do we care?

What’s so special about compactness?

• It comes up a lot in proofs of continuity, differentiation, and integration.
• It’s just a general concept which is more common than it deserves to be for how convoluted it is.