The real numbers are an ordered field

Real numbers

The set of real numbers $\mathbb{R}$ is an ordered field, meaning it’s defined as being a “tuple” of four elements, which includes

• An ordered set
• Addition operation
• Multiplication operation
• Order relation

Let’s go through each one by one.

---

Fields?

Before we define what an “ordered” field is, let’s unpack what is just an ordinary field.

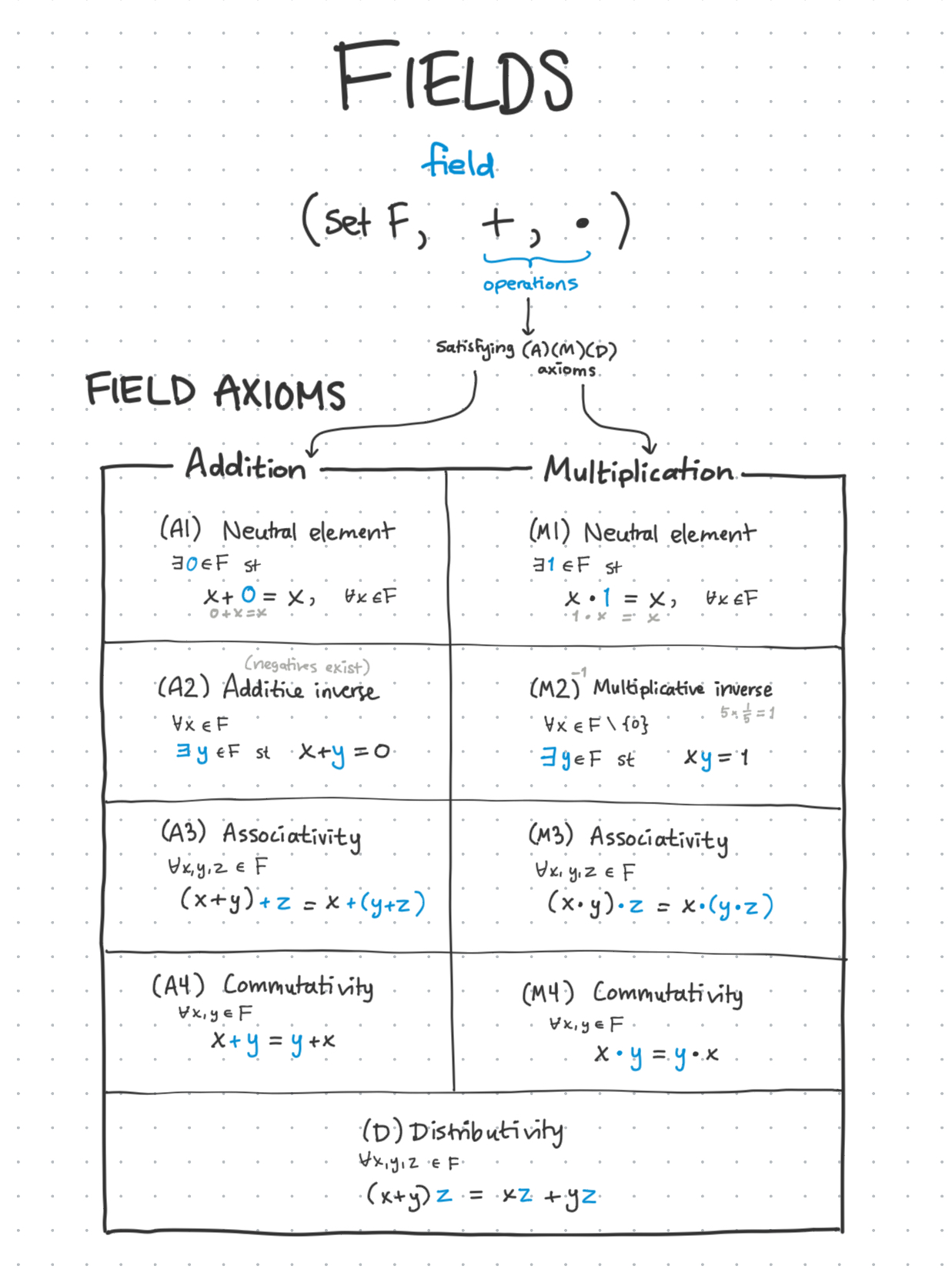
The field is a tuple of three elements, consisting of

• set
• addition operation
• multiplication operation

The two operations must satisfy the field axioms:

Basically, whatever we define as “addition” and “multiplication” better behave like addition and multiplication.

So any arbitrary operation on two elements, which satisfies these axioms (many of which we learn as children), can be called addition or multiplication.

If all these axioms are defined for all elements in the set F, we call this a valid field.

Ordered sets, relations

A set is any collection of items, ordered or not. An ordered set is a more specific type of set, whose elements can all be “ordered” in a specific way.

Example: An intuitive example can be formed from the natural numbers.

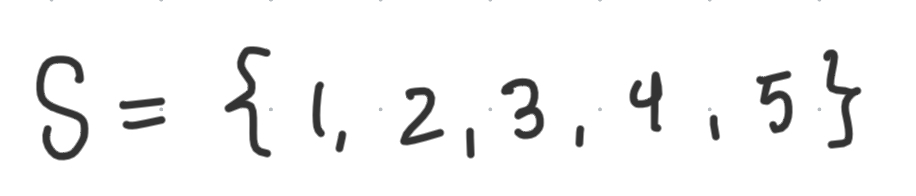
We can see that the elements in S, namely 1, 2, 3, 4, 5 can be “ordered” from least to greatest. This is consistent with our existing understanding of numbers.

With the numbers we know, it makes sense that things can be ordered. But what about for arbitrary sets? What if we had a set of triangles - could we order such a set as well?

Modern analysis is about unpacking definitions to levels of minute scrutiny, so let’s unpack what it means to be “ordered.”

Relations

A relation is anything that “relates” two elements together.

Precisely defined, it’s a subset of all possible combinations of two elements together (the cartesian product) of two sets.

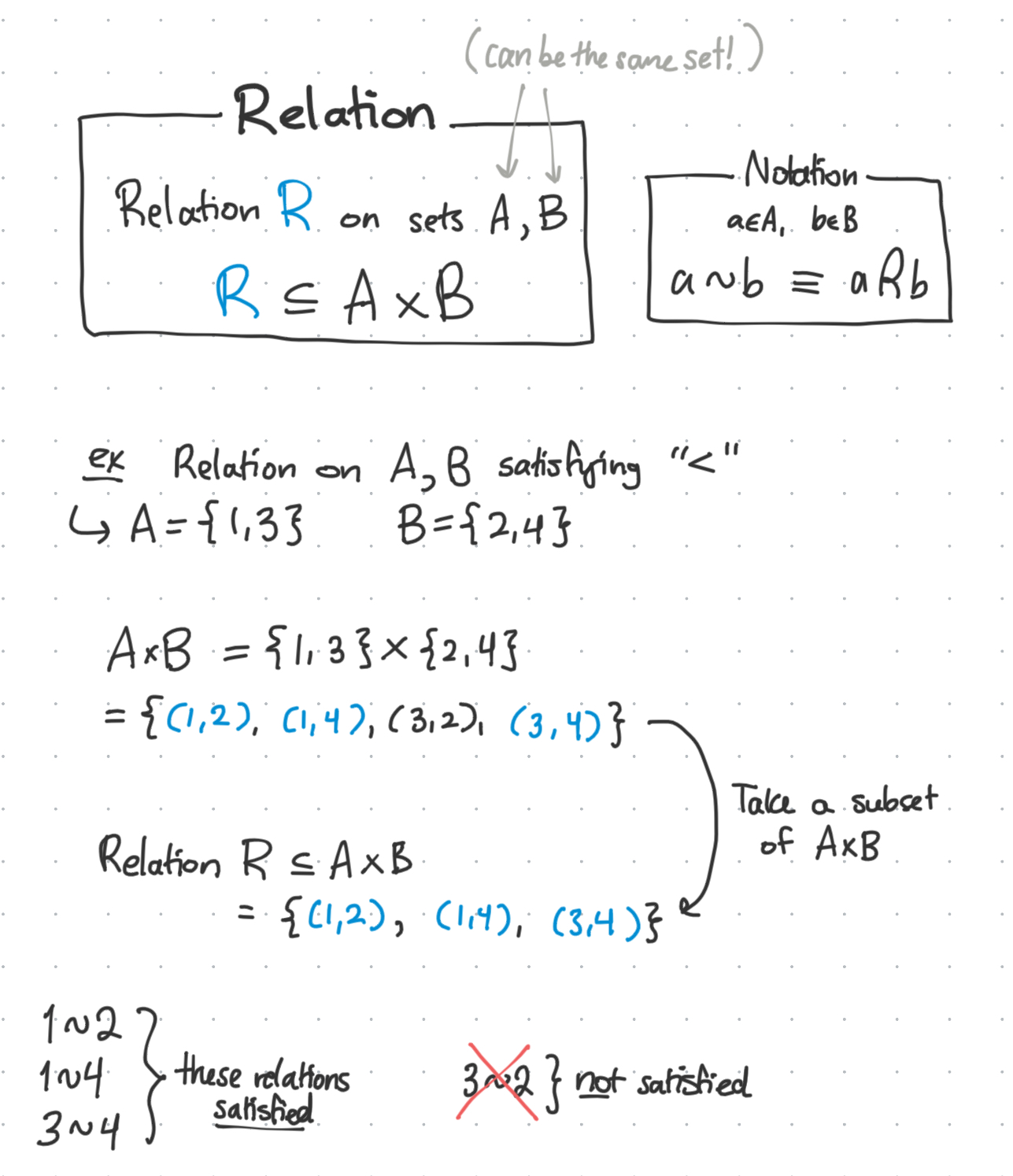
The order relation

So the “order relation” is how we precisely define what it means to be ordered. Which means that if we take the relation of an ordered set with itself, that certain subsets of the set should satisfy this ordering.

These properties are defined as such:

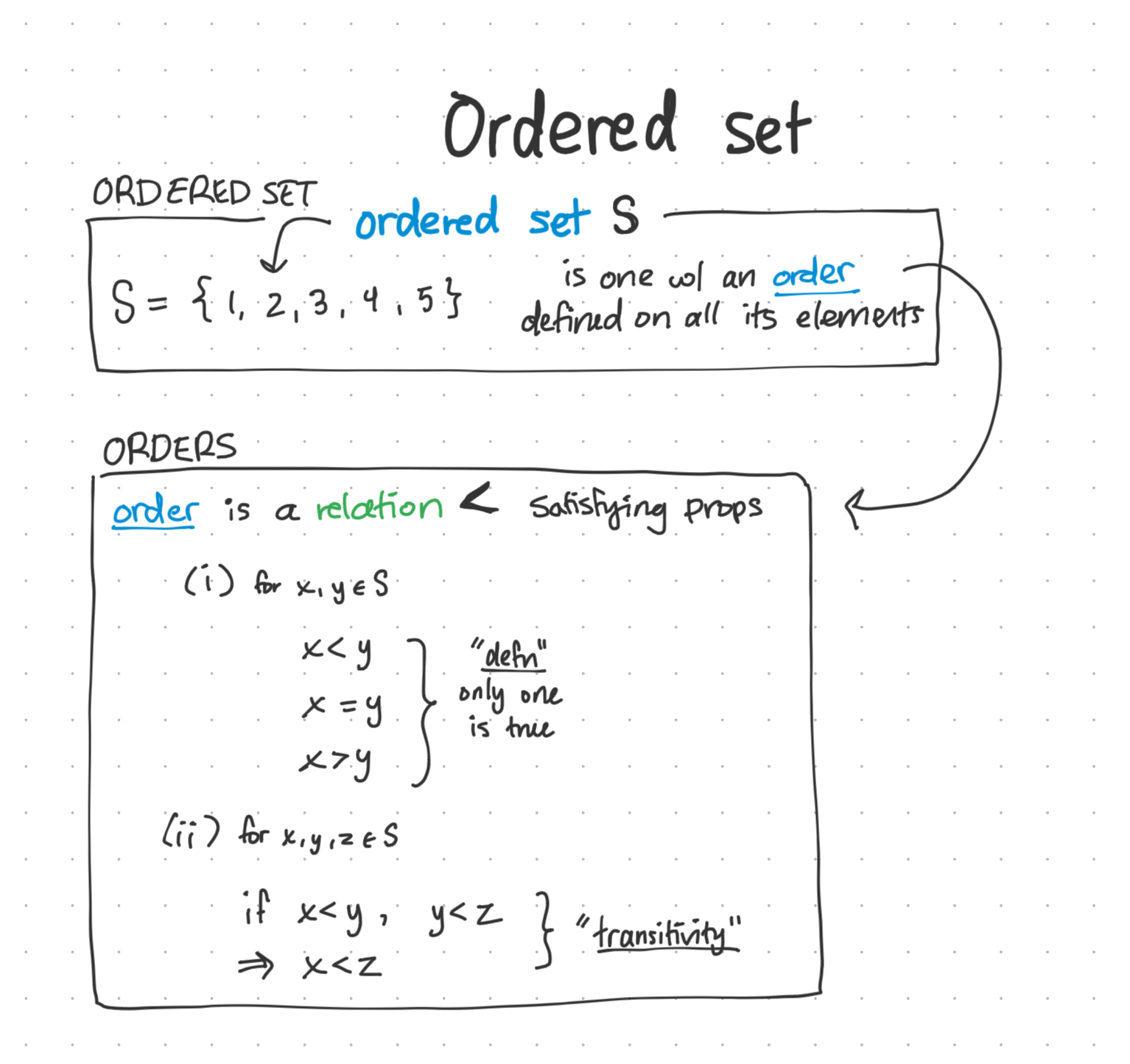
So circling back to ordering a set of triangles - if certain subsets of the triangles could satisfy these order relation properties, then we would say that set could be ordered.

Ordered field?

So back to the reals: an “ordered” field is a field with an ordered set instead of a normal one.

The reals are a complete ordered field

Edit (01/31/2025, 12:15am): Oops, I forgot that just being an ordered field isn’t enough to uniquely define the reals. For instance, the rational numbers $\mathbb{Q}$ also are an ‘ordered field’. So how do the real numbers $\mathbb{R}$ differ from $\mathbb{Q}$?

The answer is through this crucial property of $\mathbb{R}$… completeness 🙂

Completeness

Completeness is like this ‘no-holes’ property of the real numbers, where you can take ANY two elements $x, y \in \mathbb{R}$ and we can always find some squishy intermediate number $c \in \mathbb{R}$ which lies between them. $x \leq c \leq y$.

This is related to the idea that we can always keep adding more zeros after the decimal and some number at the end ‘0.00 (…) 001’ such that the number gets smaller and smaller and smaller. And that this kind of squishiness is present everywhere.

The rationals for instance have certain holes where the irrational numbers lie. So if you took the two numbers directly to the left and right of an irrational number (say, $\pi$) we would not find such a $c$ between them.

Archimedean property

There is a related property - “Dedekind completeness”, also called the “least-upper-bound” property which helps imply some other properties for our real numbers.

• All subsets of $\mathbb{R}$ that are bounded from above, have a least upper bound.

Which implies the archimedean property - that given a number $x$ we can always find some integer $y$ which is larger than $n \in \mathbb{N}$ times $x$ .

Essentially, it’s saying that the real numbers contain both infinitely large ($y>nx$) and infinitely small ($x < \frac{y}{n}$) elements.

When looked at it this way, many of us learned/taught the archimedean property to each other even as kids. Recall the highest number game where you try to name the biggest number you can. 1, 5, 42, 99, 100, 5000, 5001, 5002, 10000000, … When I was in elementary school, the game would usually end soon after someone dropped the ‘googol’ bomb. Then after getting to “googolplex” we would degenerate to “googolplex plus one”, “googolplex plus two”, …, “googolplex plus googolplex,” until we got sick of playing the game.