A foray into metric and vector spaces

The metric space bridges real analysis with topology by introducing the notion of a distance onto a set of elements. They are a general setting for studying geometry, according to Wikipedia.

Metric spaces have distances

So, the metric space is a set of elements (usually called “points”) which have a distance between any two elements in the set. Precisely, it’s a tuple $(X, d)$ consisting a set $X$ and a distance metric $d$.

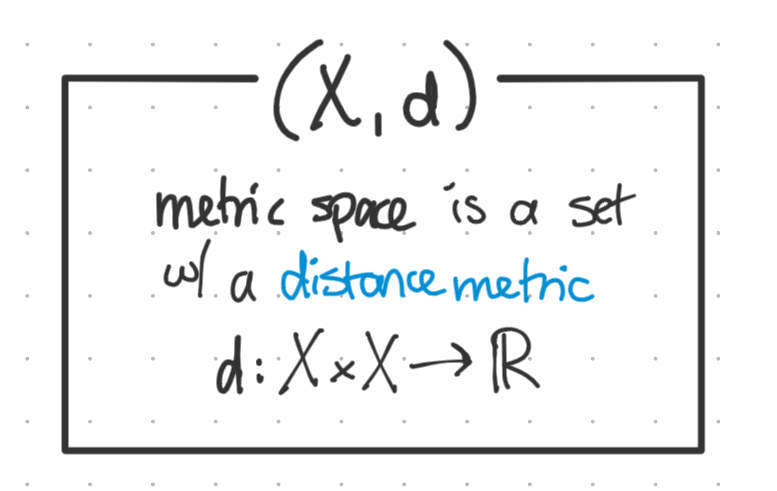
Where the distance metric is any function which satisfies these three properties:

1. Positive definiteness - All distances are either positive or zero
2. Symmetry - Order of points doesn’t affect distance
3. Triangle inequality - See below

Prop 3: Triangle inequality

Intuitively, this inequality says that any one side of a ‘triangle’ is always shorter than or equal to the sum of the other two sides.

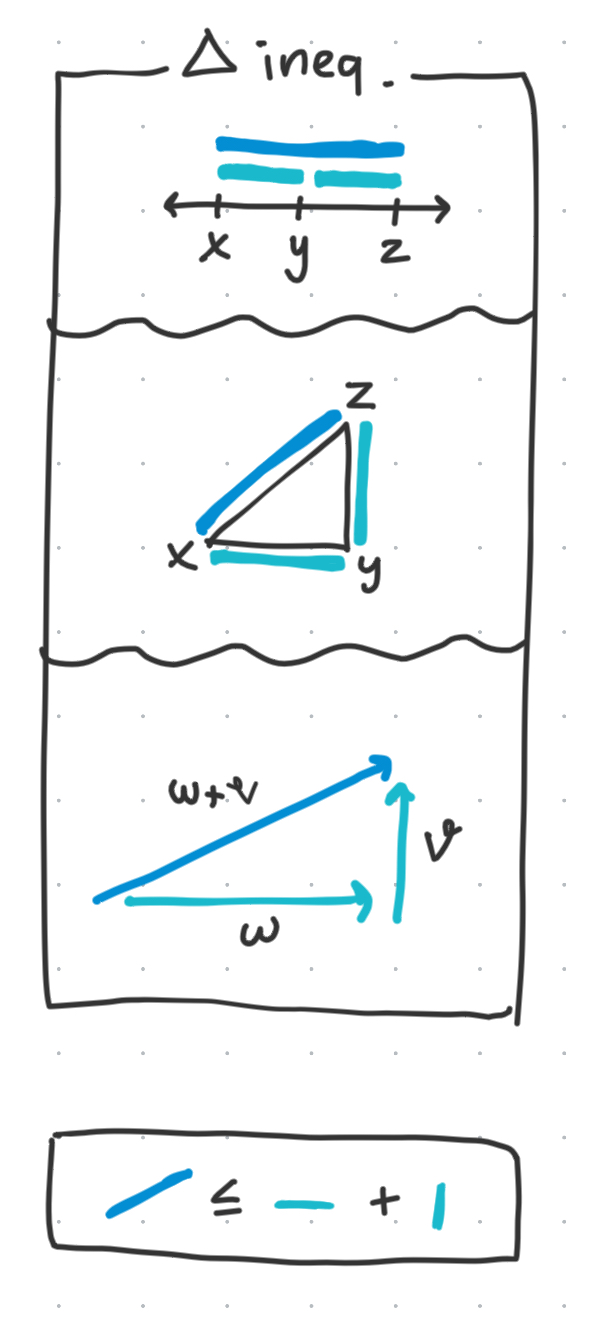
So our distance function better respect this property as well. In the case of the $\mathbb{R}$ metric space, all distances satisfy the triangle inequality in the sense that the sum of all distances making up a line segment are equal to the distance of the daddy line segment.

Vector spaces

The triangle inequality makes a little more sense in vector spaces, where we have these directed vectors pointing which can visually form a triangle.

Vector spaces are defined over a particular field (such as the reals!) and are precisely defined as a tuple containing

• a set (with elements like )
• a field, and the addition / multiplication operations.

Where the maps (addition / multiplication) have their own set of properties - which are similar to the field axioms, but slightly different in that they act upon the vectors themselves, not the elements in the field.

Some other spaces…

Normed vector spaces, inner product spaces

Here are a couple more specific types of vector spaces we learned about in class, but haven’t worked much with (and are always given definitions when doing so).

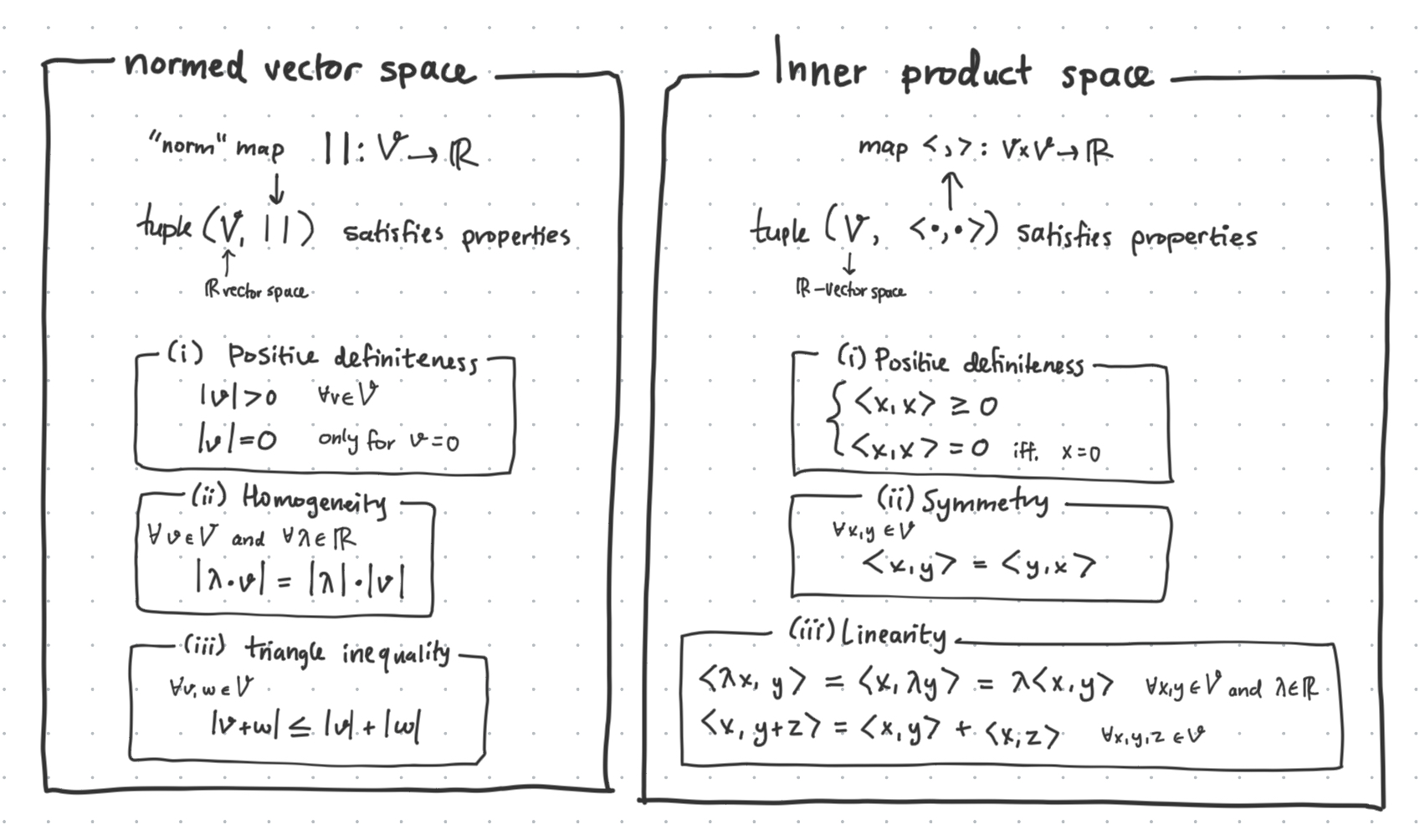
Note again the ubiquity of the triangle inequality!

Notable examples

Notably, it is good to know that euclidean space forms a normed vector space over the real numbers $\mathbb{R}^n$.

• Meaning that their distance metric is especially nice, so the distance function can distribute scalars across itself (homogeneity).

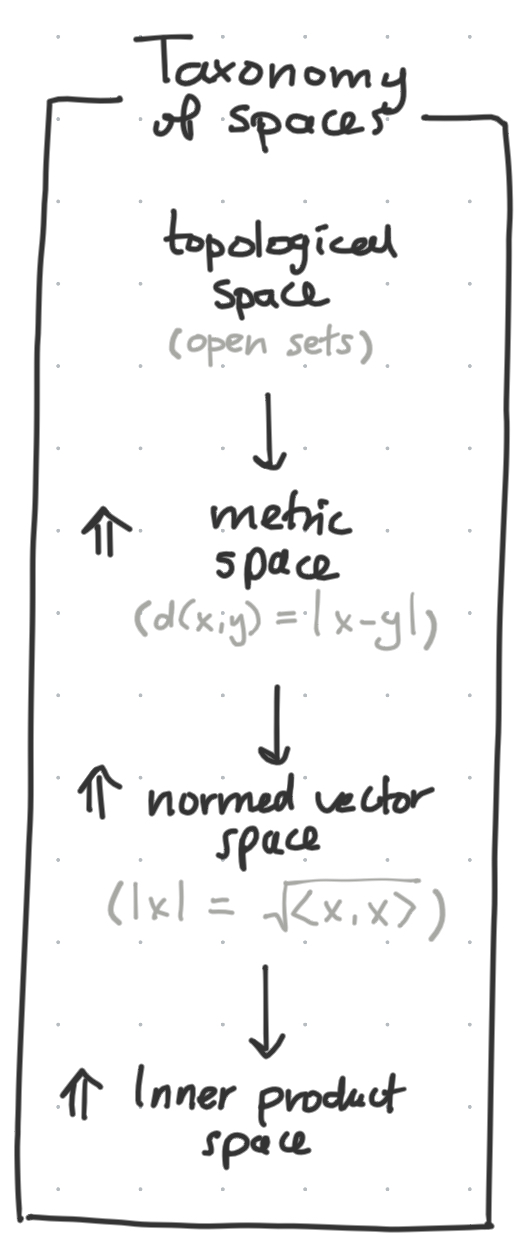
Taxonomy of spaces

To recap, here is a quick taxonomy of the different types of spaces we learned about and how they relate to each other.

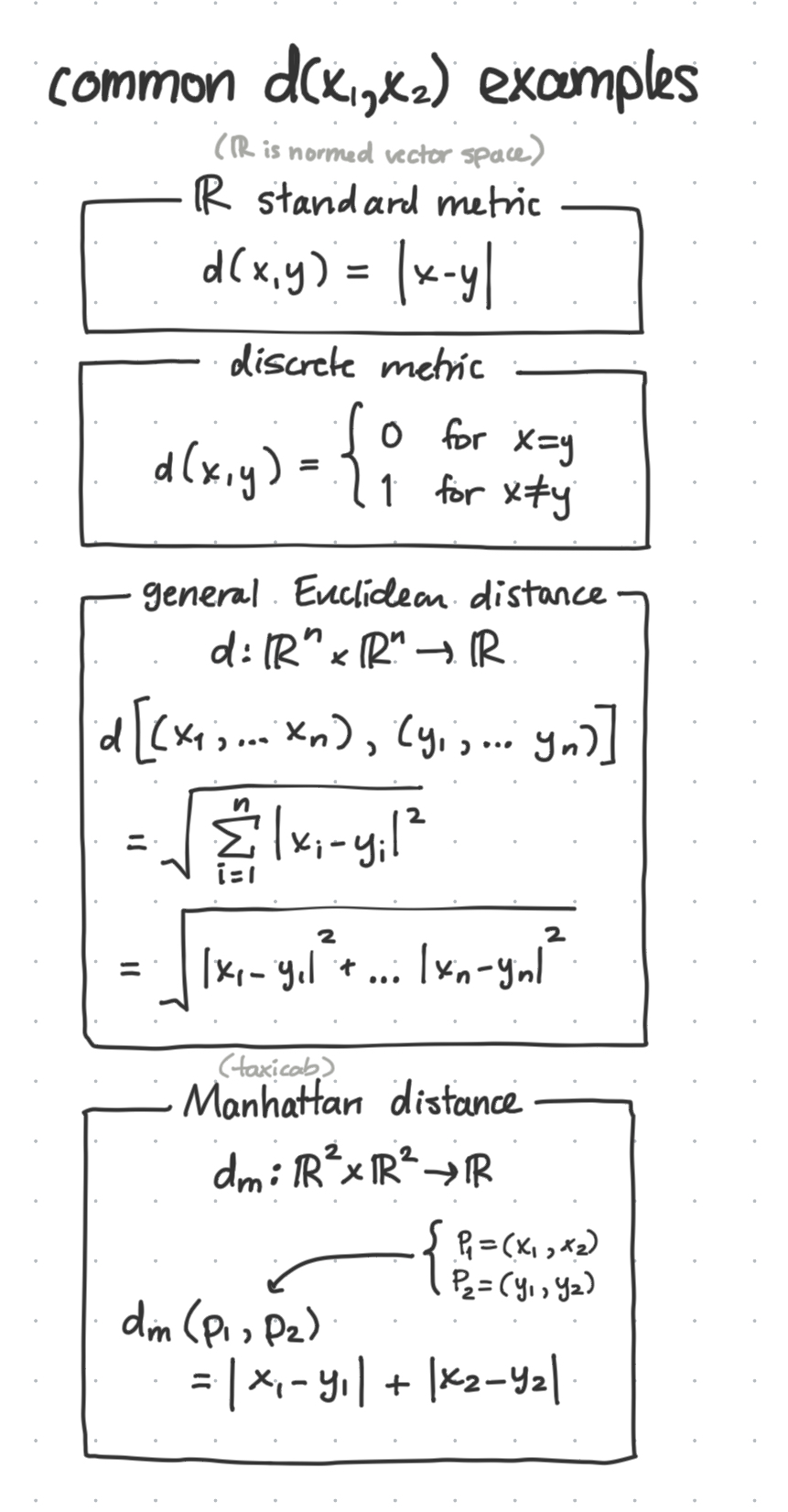
Reference: Examples of distance metrics

Some common examples of distance metrics include:

• Standard metric
• Discrete metric
• Euclidean distance (think pythagorean theorem)
• Manhattan distance (distance along a grid)